一.反向传播算法简介
二.前馈计算的过程
- 第一层隐藏层的计算
- 第二层隐藏层的计算
- 输出层的计算
三.反向传播的计算
- 计算偏导数
四.参考文献
一.反向传播算法
反向传播算法[1](Backpropagation Algorithm,简称BP算法)是深度学习的重要思想基础,对于初学者来说也是必须要掌握的基础知识,在这一小节里,我们会较为详细的介绍这一重点知识。
我们使用一个如图1所示的神经网络,该图所示是一个三层神经网络,两层隐藏层和一层输出层,输入层有两个神经元,接收输入样本 , 为网络的输出。
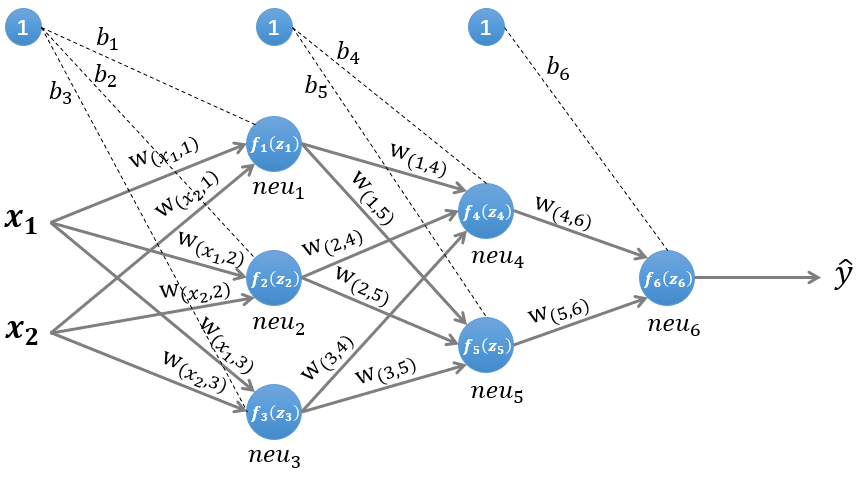
图1 一个三层神经网络
二.前馈计算的过程
为了理解神经网络的运算过程,我们需要先搞清楚前馈计算,即数据沿着神经网络前向传播的计算过程,以图1所示的网络为例:
输入的样本为:

第一层网络的参数为:
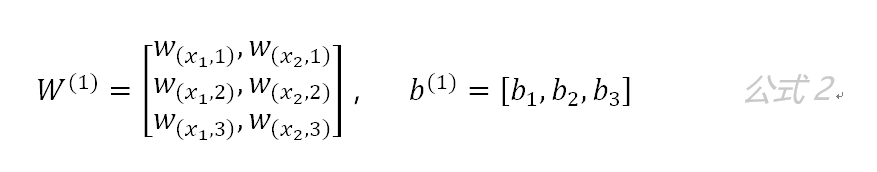
第二层网络的参数为:
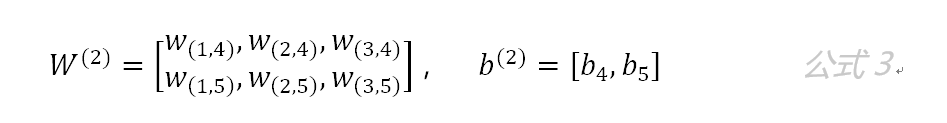
第三层网络的参数为:
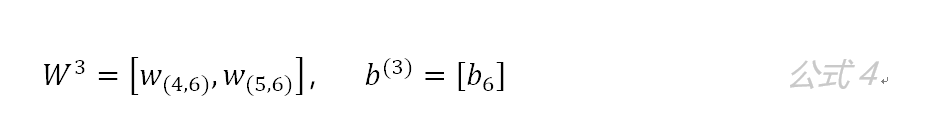
- 第一层隐藏层的计算
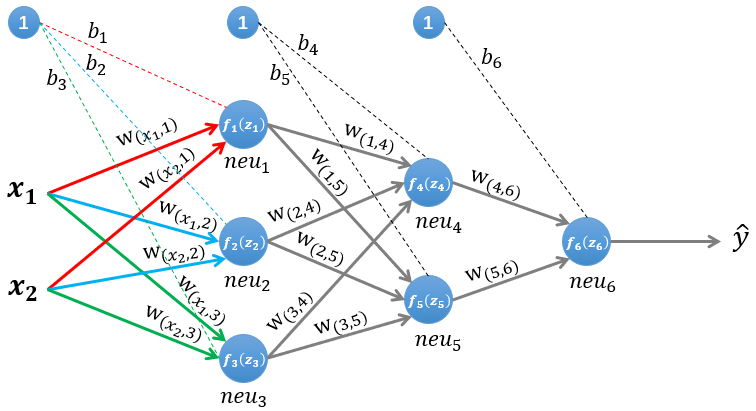
图2 计算第一层隐藏层
第一层隐藏层有三个神经元:neu1 、neu2 和neu3 。该层的输入为:
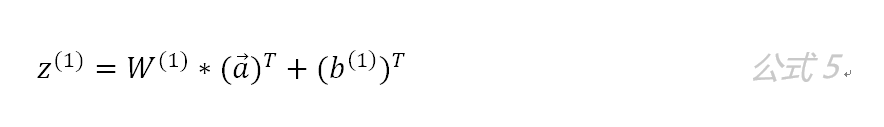
以 neu1神经元为例,则其输入为:
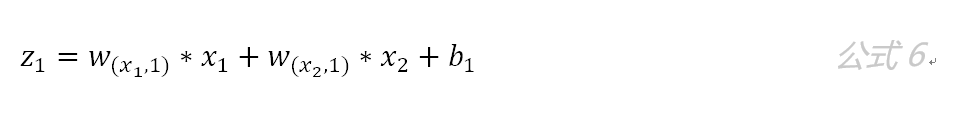
同理有:
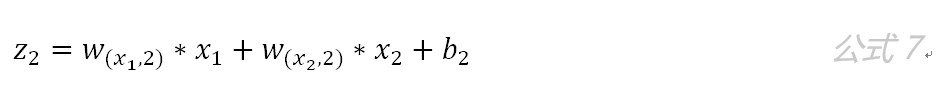
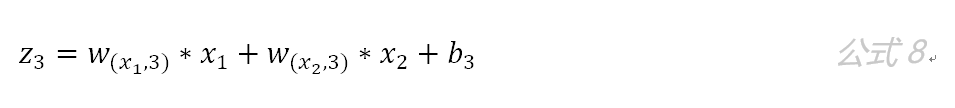
假设我们选择函数 作为该层的激活函数(图1中的激活函数都标了一个下标,一般情况下,同一层的激活函数都是一样的,不同层可以选择不同的激活函数),那么该层的输出为: f1(z1)、f2(z2) 和f3(z3) 。
·第二层隐藏层的计算
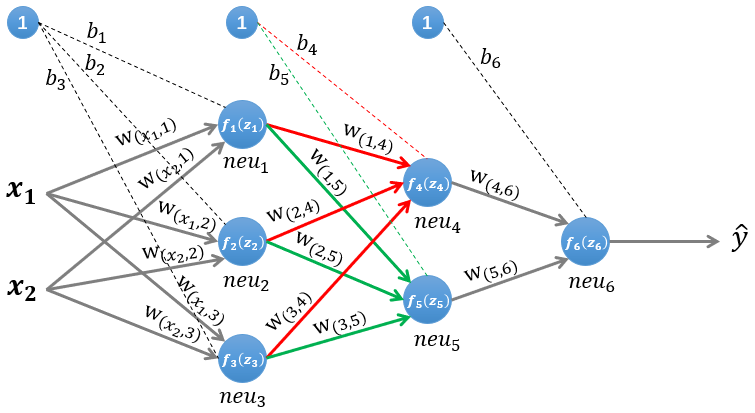
图3 计算第二层隐藏层
第二层隐藏层有两个神经元:neu4 和neu5 。该层的输入为:
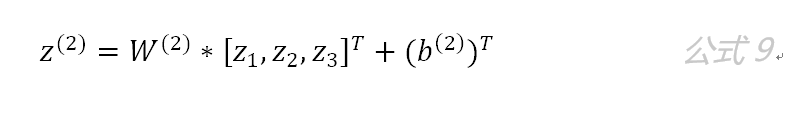
即第二层的输入是第一层的输出乘以第二层的权重,再加上第二层的偏置。因此得到 和 的输入分别为:
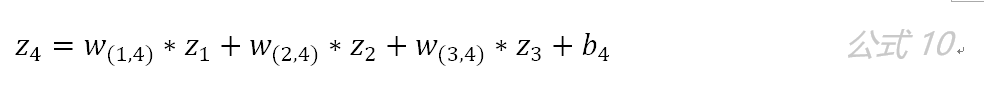
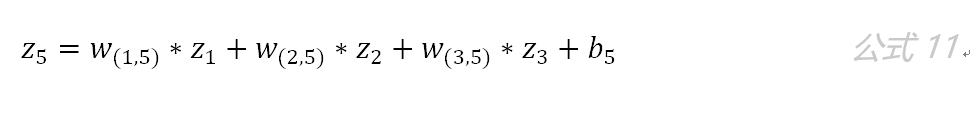
该层的输出分别为: f4(z4)和f5(z5) 。
- 输出层的计算
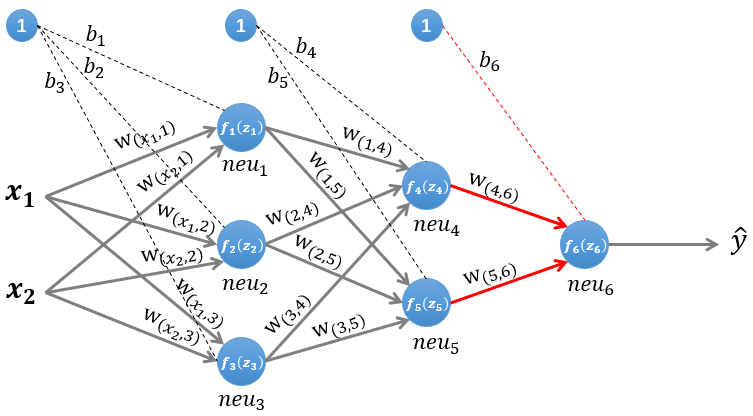
图4 计算输出层
输出层只有一个神经元:neu6 。该层的输入为:
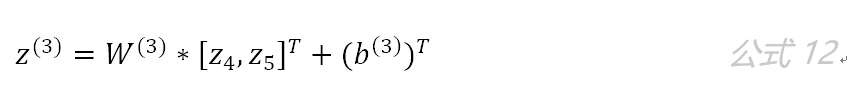
即:
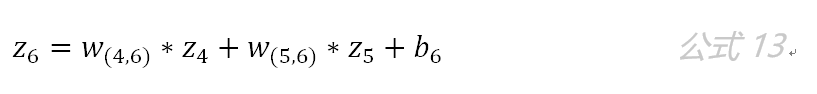
因为该网络要解决的是一个二分类问题,所以输出层的激活函数也可以使用一个Sigmoid型函数,神经网络最后的输出为: f6(z6)。
三.反向传播的计算
上一小节里我们已经了解了数据沿着神经网络前向传播的过程,这一节我们来介绍更重要的反向传播的计算过程。假设我们使用随机梯度下降的方式来学习神经网络的参数,损失函数定义为 ,其中 是该样本的真实类标。使用梯度下降进行参数的学习,我们必须计算出损失函数关于神经网络中各层参数(权重w和偏置b)的偏导数。




下面是基于随机梯度下降更新参数的反向传播算法:
输入:训练集:D={(xi,yi)}, i=1,2,….,N
学习率:γ
训练回合数(epoch):T
初始化网络各层参数w(t) 和b(t)
for t=1 …T do
打乱训练集中样本的顺序
for i=1… N do
(1)获取一个训练样本,前馈计算每一层的输入 和输出
(2)利用公式*反向传播计算每一层的误差项
(3)利用公式**和公式***计算每一层参数的导数
(4)更新参数:
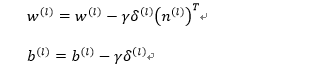
以上是BP算法的介绍,下次文章中有一个BP算法计算的完整示例,希望加深理解的读者可以跟着示例计算一遍。
四.参考文献
[1]. Learing representations by back-propagating erros.David E.Rumelhart,Geoffrey E.Hinton,Ronald J.Williams


